Paper Code Data

In this work, we explore binary classification problem under spurious correlations (prior shifts from the training to the test distribution). We discuss the formulation of four potential solutions and empirically examine the effectiveness of three methods: ERM with SGD, GDRO with Online Optimization, and GDRO with Benders Decomposition.

Our findings reveal that both Online Optimization and Benders Decomposition excel under strong spurious correlations, with Benders Decomposition slightly outperforming Online Optimization. However, ERM still demonstrates effective performance under weak spurious correlation. In terms of computational costs, Online Optimization is significantly more demanding compared to other methods. We also observe that both ERM and Online Optimization are sensitive to learning rate adjustments. Benders Decomposition, on the other hand, is insensitive w.r.t. key parameters (\(\delta\) and \(C\)). Consequently, when convexity conditions are satisfied, Benders Decomposition offers a more stable and time-efficient solution than Online Optimization and ERM under strong spurious correlation.

Main Results

(a) Training Set (\(\rho = 0.8\))
(b) ERM
(c) OnlineOpt
(d) Benders
Visualization of decision boundaries. We consider binary classification with four groups. Figures (a) to (d) display training and test sets with respective decision boundaries for ERM, OnlineOpt, and Benders. The red line represents the decision boundary where the model predicts \(y=1\) above the line and \(y=0\) otherwise. Horizontal lines indicate desirable classifiers while vertical lines indicate reliance on spurious correlations.
Comparison of three methods in binary classification by varying degrees of spurious correlation \(\rho\) from 0.5 (no correlation) to 0.9 (strong correlation). We report average and worst-group accuracies on the same test set. The highest accuracies are marked in #fff3b0.
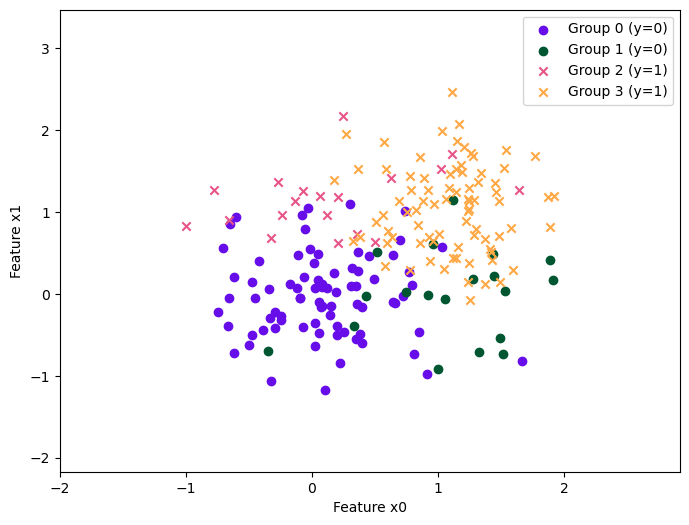
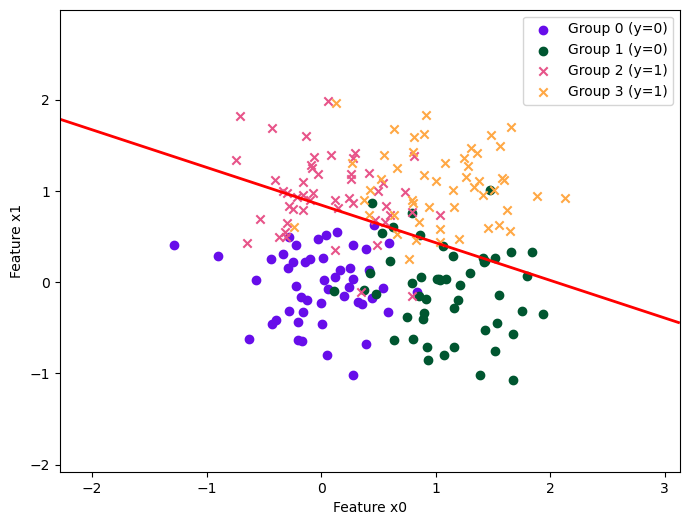
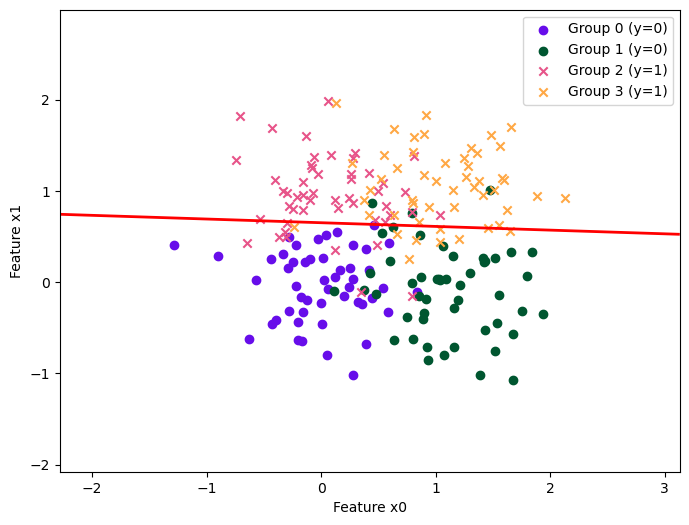
Method \(\rho = 0.5\) (unbiased) \(\rho = 0.6\) \(\rho = 0.7\) \(\rho = 0.8\) \(\rho = 0.9\)
avg acc worst acc avg acc worst acc avg acc worst acc avg acc worst acc avg acc worst acc
ERM 0.895 0.890 0.905 0.880 0.890 0.790 0.865 0.760 0.860 0.750
OnlineOpt 0.905 0.850 0.905 0.880 0.905 0.860 0.905 0.830 0.885 0.900
Benders 0.910 0.870 0.910 0.880 0.910 0.870 0.905 0.880 0.890 0.900

OnlineOpt and Benders excel under stronger spurious correlations. Across scenarios with varying \(\rho\), both OnlineOpt and Benders generally outperform or match ERM in terms of average and worst-group accuracy, except in cases with minimal prior shifts from the training to the test distribution. Notably, the performance gap between ERM and the other two methods widens as \(\rho\) increases, indicating a decrease in ERM's robustness under stronger spurious correlations.

Benders marginally surpasses OnlineOpt across all settings. OnlineOpt and Benders demonstrate similar performance in terms of average and worst-group accuracies. However, Benders exhibits a slight advantage over OnlineOpt consistently in all the tasks evaluated.

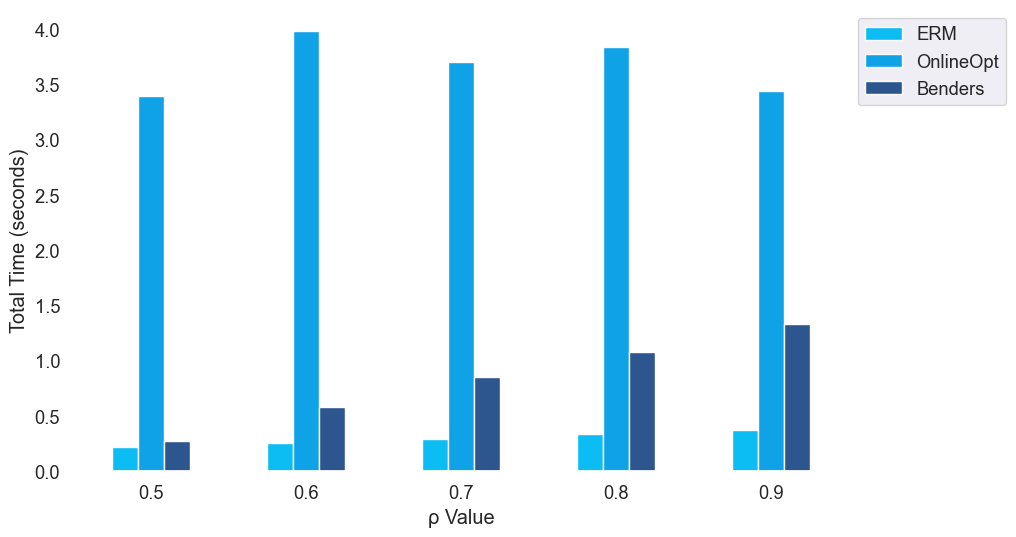
Total time (seconds) of three methods under different degrees of spurious correlation \(\rho\).

OnlineOpt incurs the highest time complexity. We calculate the total training time for methods under various \(\rho\) levels. We can see that ERM is the most computationally efficient one, consistently outperforming OnlineOpt and Benders across various \(\rho\) levels. OnlineOpt incurs the highest computational duration, which suggests its substantial complexity. Benders is more efficient than OnlineOpt but still lags behind ERM, particularly when spurious correlation intensifies. This highlights the trade-off between computational efficiency and robustness against varying degrees of spurious correlations for these methods.

Ablation Studies

Accuracies of ERM for different learning rates
Accuracies of OnlineOpt for different learning rates
Accuracy comparison of ERM vs OnlineOpt for different learning rates. OnlineOpt outperforms ERM across different learning rates in general. ERM is more sensitive to learning rate than Online Optimization.

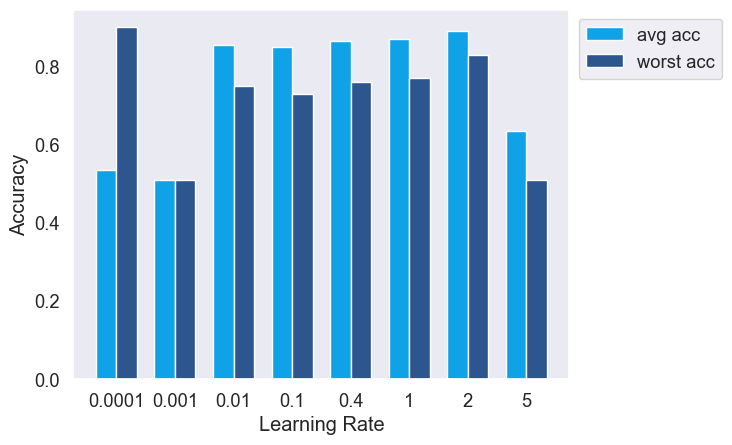
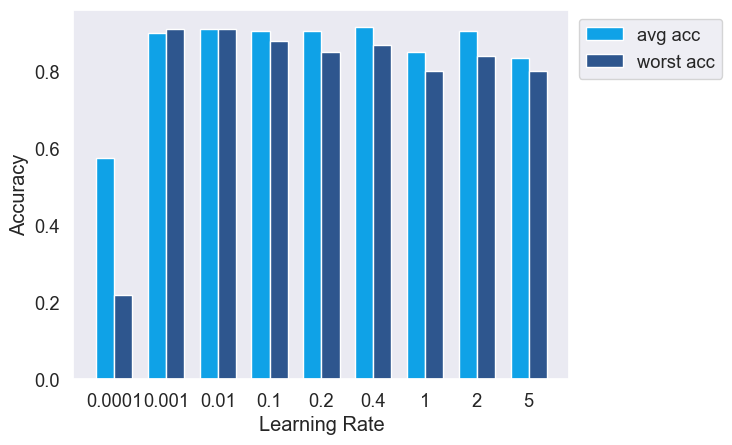
Sensitivity of ERM and OnlineOpt to learning rate. 1) ERM is sensitive to changes in the learning rate, exhibiting notable variations in both average and worst group accuracies across different rates. 2) In contrast, OnlineOpt demonstrates considerably less sensitivity to learning rate adjustments, with the exception of a very small learning rate (0.0001). This suggests an advantage of OnlineOpt, as it does not require as meticulous a calibration of the learning rate compared to ERM.

Accuracies of ERM for different batch sizes
Accuracies of OnlineOpt for different batch sizes
Comparative analysis of ERM and OnlineOpt across various batch sizes. Both methods exhibit robustness to batch size variations. ERM demonstrates a more versatile range in batch size adaptability, in contrast to OnlineOpt constrained by the size of the smallest group.

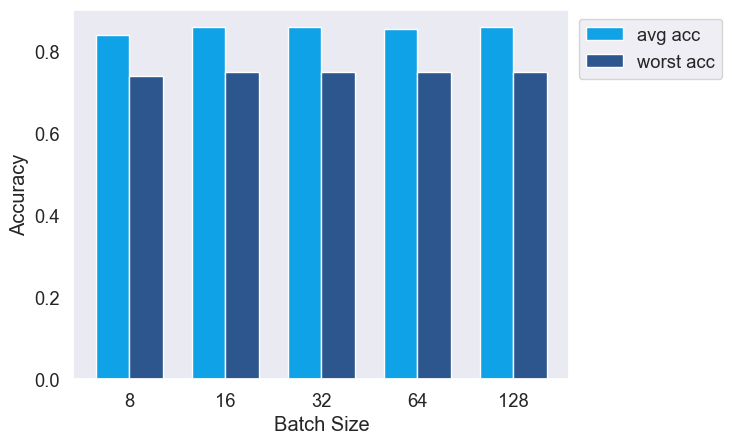
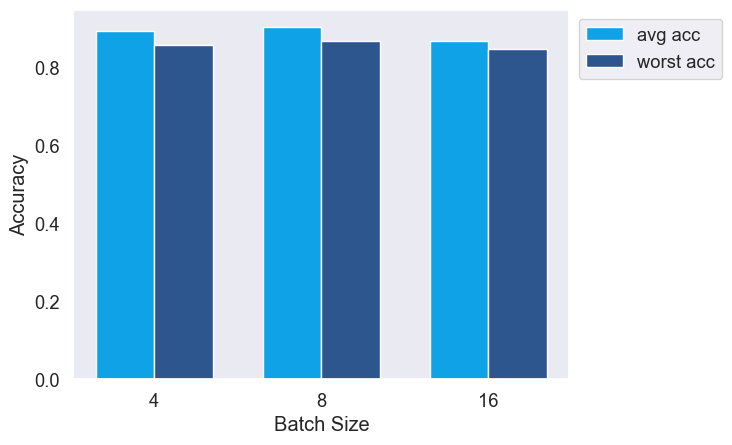
ERM and OnlineOpt are stable across various batch sizes.

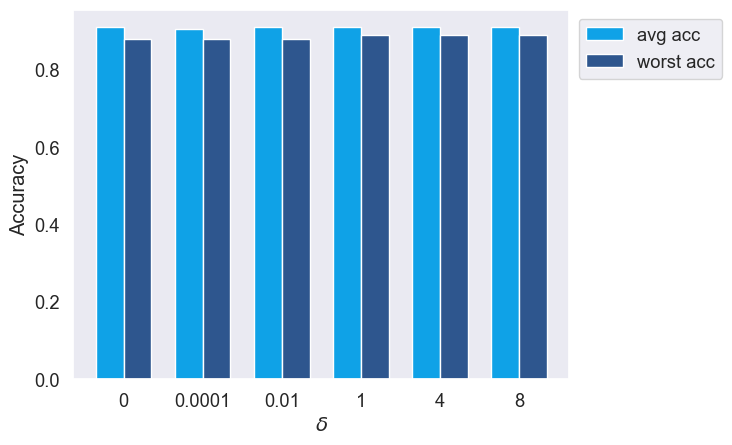
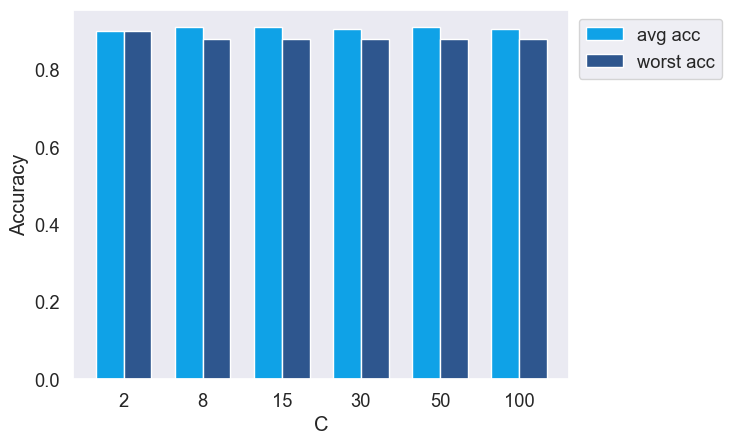
Accuracies of Benders for different \(\delta\)
Accuracies of Benders for different \(C\)

Benders is robust to parameters \(\delta\) and \(C\), which are the only parameters in this method.